Challenge 1 : Introduction aux circuits quantiques

from machinerie import Circuit, draw404
from math import pi

draw404()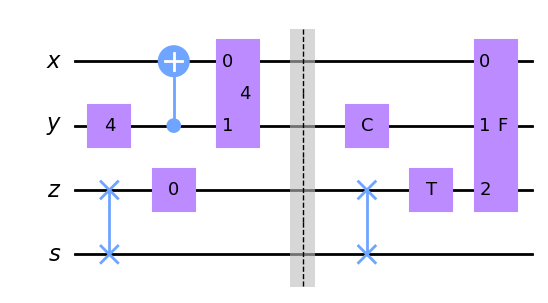

Introduction aux outils

Si le mot qubit vous donne le vertige, je vous invite à prendre cinq minutes pour regarder une introduction aux ordinateur quantiques, par exemple : https://youtu.be/bayTbt_8aNc. Cependant, pas d’inquiétude, le doctorat en phyisque n’est pas nécessaire pour résoudre ces challenges, les notions nécessaires seront rapidement expliquées.

Représentation

On peut le représenter sous plusieurs formes, par exemple, en utilisant une sphère de Bloch:

qc = Circuit(1)
qc.draw_qubits("bloch")

Pour facilier les choses, nous allons dans cette suite de challenges uniquement manipuler des circuits. Pour représenter le qubit $|0\rangle$, on utilise donc un circuit vide à 1 qubit: Circuit(1).

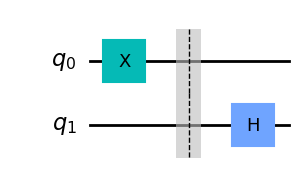
Pour créer l’état $|1\rangle$, on peut appliquer une porte NOT:

qc = Circuit(1)
qc.x(0)
qc.draw_qubits("bloch")

Plus généralement, utiliser la porte u de qiskit permet de créer n’importe quel état.

qc = Circuit(1)
qc.u(theta=pi / 4, phi=-pi / 4, lam=0, qubit=0)
qc.draw_qubits("bloch")

Qiskit permet aussi un rendu Latex:

qc = Circuit(1)
qc.h(0)
qc.draw_qubits()

\[\frac{\sqrt{2}}{2} |0\rangle+\frac{\sqrt{2}}{2} |1\rangle\]

Une autre façon d’écrire nos qubits est d’utiliser des vecteurs. Par exemple, pour la base canonique: \[ |0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \space |1\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \] Dans ce cas là, le qubit précédent s’écrit: \[ \frac{\sqrt{2}}{2} |0\rangle + \frac{\sqrt{2}}{2} |1\rangle = \frac{\sqrt{2}}{2} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \]

Mesure

L’action de mesure sur le qubit le sort de son état quantique, il s’effondre <_<, il ne peut prendre qu’une valeur classique, 0 ou 1. Dans le cas des qubits $|0\rangle$ et $|1\rangle$, lors d’une mesure, ils donneront toujours 0, et 1. Mais quid des qubits en superposition ? Pour un qubit en superposition, la mesure est probabiliste. Pour un qubit $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$, les probabilités de mesure sont données par:

\[ \Pr(0) = \left|\alpha\right|^2, \space \Pr(1) = \left|\beta\right|^2 \]

Dans le cas de $|\psi\rangle = \frac{\sqrt{2}}{2} |0\rangle + \frac{\sqrt{2}}{2} |1\rangle$, la probabilité d’obtenir 0 ou 1 est la même, $\frac{1}{2}$!

qc = Circuit(1)
qc.h(0)
qc.draw_qubits()

\[\frac{\sqrt{2}}{2} |0\rangle+\frac{\sqrt{2}}{2} |1\rangle\]

qc.get_measure(shots=1000, normalise=False)

{'0': 505, '1': 495}

Systèmes multiples

\[ |00\rangle = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}, \space |01\rangle = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}, \space |10\rangle = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}, \space |11\rangle = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \]

Pour combiner des qubits, on utilise l’opération $\otimes$: \[ |00\rangle = |0\rangle \otimes |0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}\otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \times \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ 0 \times \begin{pmatrix} 1 \\ 0 \end{pmatrix} \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \]

En pratique cela donne:

qc = Circuit(2)  # Circuit à 2 qubits
qc.h(0)  # On applique une porte H au 1er qubit
qc.draw_qubits()

\[\frac{\sqrt{2}}{2} |00\rangle+\frac{\sqrt{2}}{2} |01\rangle\]

Attendez une seconde, n’aurait-on pas dû obtenir $\left(\frac{\sqrt{2}}{2} |0\rangle + \frac{\sqrt{2}}{2} |1\rangle \right) \otimes |0\rangle = \frac{\sqrt{2}}{2} |00\rangle + \frac{\sqrt{2}}{2} |10\rangle$?

Cela est dû à qiskit, l’ordre est inversé, le qubit 0, celui en haut du circuit, est représenté en dernier. L’opération précédente était en fait $|0\rangle \otimes \left(\frac{\sqrt{2}}{2} |0\rangle + \frac{\sqrt{2}}{2} |1\rangle \right)$, ce qui donne bien le résultat obtenu en pratique: $\frac{\sqrt{2}}{2} |00\rangle + \frac{\sqrt{2}}{2} |01\rangle$, ouf.

Portes simples

Les portes peuvent être représentés par des matrices unitaires, que l’on applique sur nos états quantiques: \[ |\psi_{\text{out}}\rangle = U|\psi_{\text{in}}\rangle \]

Par exemple, la porte quantique NOT, notée $X$, qui reproduit le même comportement que son équivalent classique: \[ X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \] \[ X|0\rangle = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} = |1\rangle, \] \[ X|1\rangle = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} = |0\rangle \]

qc = Circuit(1)
qc.x(0)
qc.draw_circuit()

Nous avons aussi vu la porte $H$, c’est la porte de Hadamard, elle permet de créer des états superposés: \[ H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}, \] \[ H|0\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix}, \] \[ H|1\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ -1 \end{pmatrix} \]

Ce qui peut se décomposer selon la base canonique, pour voir le lien entre la notation braket et la notation matricielle: \[ H|0\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \frac{1}{\sqrt{2}} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \frac{1}{\sqrt{2}} |0\rangle + \frac{1}{\sqrt{2}}|1\rangle \]

qc = Circuit(1)
qc.h(0)
qc.draw_circuit()

Pour se déplacer sur la sphère de Bloch, on peut utiliser les portes $RX$, $RY$ et $RZ$. Elles sont définies par:

$$ R_X() = \[\begin{pmatrix} \cos\frac{\theta}{2} & -i\sin\frac{\theta}{2} \\ -i\sin\frac{\theta}{2} & \cos\frac{\theta}{2} \end{pmatrix}\]

R_Y() = \[\begin{pmatrix} \cos\frac{\theta}{2} & -\sin\frac{\theta}{2} \\ \sin\frac{\theta}{2} & \cos\frac{\theta}{2} \end{pmatrix}\]

R_Z() = \[\begin{pmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}} \end{pmatrix}\]

qc = Circuit(1)
qc.rx(theta=pi / 3, qubit=0)
qc.ry(pi / 6, 0)
qc.rz(pi / 12, 0)
qc.draw_circuit()

Ces notations permettent facilement d’appliquer des portes à un qubit, sur un qubit, mais qu’en est-il des états à plusieurs qubits ? Pour appliquer des portes simples dans des systèmes multiples, il faut utiliser le produit tensoriel. Par exemple, dans un système à deux qubits, appliquer la porte $H$ sur le premier qubit uniquement est équivalent à appliquer $H$ sur le premier qubit, et l’identité sur le second. Cela nous permet de créer une porte de la bonne taille: \[ H \otimes I = \frac{1}{\sqrt{2}}\begin{pmatrix}1 & 1 \\ 1& -1\end{pmatrix} \otimes \begin{pmatrix} 1&0 \\ 0& 1 \end{pmatrix} = \frac{1}{\sqrt{2}}\begin{pmatrix} 1\times\begin{pmatrix} 1&0 \\ 0& 1 \end{pmatrix}&1\times\begin{pmatrix} 1&0 \\ 0& 1 \end{pmatrix}\\1\times\begin{pmatrix} 1&0 \\ 0& 1 \end{pmatrix}&-1\times\begin{pmatrix} 1&0 \\ 0& 1 \end{pmatrix} \end{pmatrix}= \frac{1}{\sqrt{2}}\begin{pmatrix} 1&0&1&0\\0&1&0&1\\1&0&-1&0\\0&1&0&-1\end{pmatrix} \]

Ce qui nous permet de l’utiliser sur notre système multiple. Par exemple, pour l’appliquer sur $|01\rangle$: \[ (H \otimes I) |01\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix} 1&0&1&0\\0&1&0&1\\1&0&-1&0\\0&1&0&-1\end{pmatrix} \begin{pmatrix} 0\\1\\0\\0\end{pmatrix} = \frac{1}{\sqrt{2}}\begin{pmatrix} 0\\1\\0\\1\end{pmatrix} = \frac{1}{\sqrt{2}} |01\rangle + \frac{1}{\sqrt{2}} |11\rangle \]

La notation avec des brakets permet aussi de rester sur un seul qubit à la fois. Pour appliquer $H$ au premier qubit uniquement: \[ (H|0\rangle) \otimes |1\rangle = \left(\frac{1}{\sqrt{2}} |0\rangle + \frac{1}{\sqrt{2}} |1\rangle \right) \otimes |1\rangle = \frac{1}{\sqrt{2}} |01\rangle + \frac{1}{\sqrt{2}} |11\rangle \]

qc = Circuit(2)

# Préparation de l'état |01>
qc.x(0)
qc.barrier()

# La barrière n'a pas d'impact sur le circuit (ici), je l'utiliserai pour améliorer la lisibilité des circuits.

# On applique ensuite H
qc.h(1)
qc.draw_circuit()

qc.draw_qubits()

\[\frac{\sqrt{2}}{2} |01\rangle+\frac{\sqrt{2}}{2} |11\rangle\]

Portes multiples

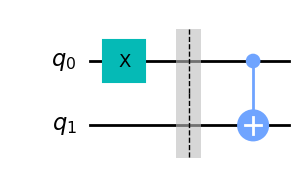
Une porte qui va beaucoup nous intéresser par la suite est la CNOT, ou controlled-NOT. C’est elle qui va permettre d’intriquer des qubits ! Elle agit sur une paire de qubit, si le premier est à 0 (qubit de contrôle), il ne se passe rien, par contre si le premier est à 1, le deuxième est inversé, il passe par une porte NOT. Elle est définie par :

\[ \text{CNOT} = \begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{pmatrix} \] Ou encore : \[ \text{CNOT} = \begin{cases} |00 \rangle \xrightarrow[]{I \otimes I} |00 \rangle \\ |01 \rangle \xrightarrow[]{I \otimes I} |01 \rangle \\ |10 \rangle \xrightarrow[]{I \otimes NOT} |11 \rangle \\ |11 \rangle \xrightarrow[]{I \otimes NOT} |10 \rangle \end{cases} \]

qc = Circuit(2)

qc.x(0)
qc.barrier()

qc.cx(0, 1)  # Le qubit de contrôle est 0, celui qui va être inversé est 1
qc.draw_circuit()

qc.draw_qubits()

\[ |11\rangle\]

Dans le cas de qubits en superposition, j’utilise la notation avec braket qui permet de voir facilement le résultat:

\[ \text{CNOT} \left(\frac{1}{\sqrt{2}} |00\rangle + \frac{1}{\sqrt{2}} |10\rangle \right) = \frac{1}{\sqrt{2}} \text{CNOT} |00\rangle + \frac{1}{\sqrt{2}} \text{CNOT} |10\rangle = \frac{1}{\sqrt{2}} |00\rangle + \frac{1}{\sqrt{2}} |11\rangle \]

qc = Circuit(2)

qc.h(0)
qc.barrier()

qc.cx(0, 1)
qc.draw_circuit()

qc.draw_qubits()

\[\frac{\sqrt{2}}{2} |00\rangle+\frac{\sqrt{2}}{2} |11\rangle\]

Un dernier point pour la route : opérations avec les bra-kets et décomposition spectrale

Sans rentrer dans les détails, la forme des brakets a une utilité autre que nous rallentir à l’écriture : elle sert à représenter les opérations usuelles de manière visuelle.

Par exemple, un produit scalaire (complexe) : $u^\dagger v$, peut s’écrire : \[ \langle u | v \rangle \]

De la même manière, le produit : $u v^\dagger$ s’écrit : \[ | u \rangle \langle v | \]

Exemple d’écriture matricielle: \[ | 1 \rangle \langle 0 | = \begin{pmatrix} 0 &0\\ 1&0\end{pmatrix} \]

Cette notation vas nous être utile pour décomposer nos portes. Commes toutes les portes sont des matrices unitaires, elles satisfont: \[ UU^\dagger = I = U^\dagger U \]

Le théorème spectral nous donne donc une base orthonormale de dimension $N$: $\{|\psi_1\rangle, \ldots, |\psi_N\rangle\}$, avec les vecteurs propres $\lambda_1, \ldots, \lambda_N$ such that $U = \lambda_1 |\psi_1\rangle\langle\psi_1| + \cdots + \lambda_N |\psi_N\rangle\langle\psi_N|$.

Ou encore \[ U = \sum_{k=1}^N \lambda_k |\psi_k\rangle\langle\psi_k| \tag{1} \]

Par exemple pour l’identité:

\[I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = |0\rangle \langle 0| |1\rangle \langle 1|\]

Note (non nécessaire) sur l’intrication

Une propriété très intéressante des qubits est qu’ils peuvent être séparés, mais aussi intriqués, c’est-à-dire qu’ils sont dépendants les uns des autres. Cela permet, par exemple, d’agir sur un qubit et d’obtenir des informations sur le second.

Si l’on prend l’état intriqué $|\psi\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)$, et que l’on mesure le premier qubit, on a 50% de chance d’obtenir $0$ et 50% d’obtenir $1$. Cependant, en mesurant uniquement le premier qubit, l’état du second est entièrement déterminé sans qu’il soit mesuré ! En effet, si l’on mesure $0$ pour le premier qubit, alors le second est nécessairement aussi $0$. Attention, comme la mesure du premier qubit est aléatoire, cela ne permet pas de téléporter des informations à une vitesse supérieure à celle de la lumière, car dans l’autre perspective, on ne connaît pas l’état de la mesure (avant de recevoir l’information par un canal classique, par exemple).

Un contre-exemple est l’état $|\psi\rangle = \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \otimes \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$. La mesure du premier qubit ne donne aucune information sur le second ; les deux qubits sont indépendants ou séparables.

À vous de jouer !

Vous n’aurez besoin uniquement des portes présentées au dessus: $X$, $H$, $RX$, $RY$, $RZ$, $CNOT$, cependant, toute la librairie est disponible (l’API de vérification accepte n’importe quel Circuit de bonne taille).

Partie 1: Rotation

On a vu que l’état $H|0\rangle$ a une probabilité $\frac{1}{2}$ de donner 0, et $\frac{1}{2}$ de donner 1. On peut en réalité trouver un état pour n’importe couple de probabilité donné.

Trouvez un état $|\psi\rangle$ ayant une probabilité $\frac{1}{4}$ de donner 0, et $\frac{3}{4}$ de donner 1.

p1 = Circuit(1)
p1.draw_circuit()

p1_input = Circuit(1)

p1_input.x(0)
p1_input.rx(pi / 3, 0)
p1_input.get_measure()

{'0': 0.2470703125, '1': 0.7529296875}

p1.compose(p1_input, front=True, inplace=True)  # oui, inutile ici
print(p1.get_measure(shots=10000))
print("{'1': ~0.75, '0': ~0.25}")

{'0': 0.2521, '1': 0.7479}
{'1': ~0.75, '0': ~0.25}

Partie 2: Vecteurs propres

Pour l’opération NOT, un vecteur propre est l’état $|+\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix}$, associé à la valeur propre $1$: $X |+\rangle = |+\rangle$. L’état $|+\rangle$ peut se construire avec une porte de Hadamard: $H|0\rangle = |+\rangle$.

Trouvez un vecteur propre de $\text{CNOT}(I\oplus H)$, représenté en circuit ci-dessous :

p2 = Circuit(2)
p2.h(0)
p2.cx(0, 1)
p2.draw_circuit()

p2_input = Circuit(2)

p2_input.ry(pi / 4, 0)
p2_input.h(1)

p2.compose(p2_input, front=True, inplace=True)
p2.draw_circuit()

# Vérification
print(f"""
    {p2_input.get_measure()}
~=
    {p2.get_measure()}
""")


    {'10': 0.4267578125, '00': 0.4130859375, '11': 0.0771484375, '01': 0.0830078125}
~=
    {'00': 0.462890625, '10': 0.40625, '01': 0.0615234375, '11': 0.0693359375}

Récupération du drapeau !

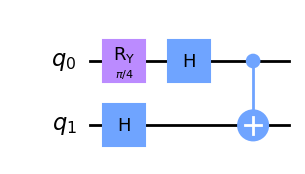
Pour valider vos circuits p1_input et p2_input, il faut me les envoyer sous forme flat, à l’adresse donée dans l’énoncée. Le code suivant devrait se charger des détails. Vérifiez l’URL.

Le brute force est interdit, vous avez des tests pour vérifier de votre côté. Cependant, même avec $10000$ shots, il se peut que vous soyez très malchanceux, dans ce cas là, n’hésitez pas à réessayer une ou deux fois. Si le problème persiste, que vous pensez avoir juste et que c’est l’API qui est cassé, ce qui est tout à fait possible, venez me voir en DM sur discord : (sckathach?), ou Le magicien quantique.

import requests
import json

data = {
    "p1_input": p1_input.get_flat_unitary(),
    "p2_input": p2_input.get_flat_unitary(),
}

url = "https://causapscal-des-profondeurs.404ctf.fr/challenges/1"
headers = {"Content-Type": "application/json", "Accept": "application/json"}
response = requests.post(url, json=data, headers=headers)

print(json.loads(response.content)["message"])

GG ! Voici le drapeau : 404CTF{uN3_SUp3rp0s1tIon_d3_dr4pE4ux_PoUr_1_m3l4nGE_ExPl0S1f}